C言語でレイトレーシングプログラムを作った
初めに
C言語で3Dゲームを作ったという記事の中で言及した通り, 42のLv2ではレイキャスティングで3Dゲームを作る cub3D と, レイトレーシングプログラムを作る miniRT という課題の2つがあり, 自分は cub3D を選択した.
しかし, レイトレーシングもやってみたくなったので, 課題の提出こそしないが, 自分なりにminiRTをやってみた. この記事はその解説記事です.
なお課題の提出はしてないのでこれで合っているかどうかは保証しかねる. 間違いがあればコメントかTwitter, Discordなどで連絡ください.
ではやっていくぞー.
miniRTの概要
具体的なコードやアルゴリズムの説明の前にまずはminiRTの課題の概要から.
miniRT の課題を一言で表すと「C言語でレイトレーシングプログラムを作りましょう」って感じ.
具体的に満たす必要のある仕様は以下の通りである.
.rt拡張子のファイル(以降 rtファイル と呼ぶ)を受け取り, そのファイルに記載された設定を元にウィンドウに画像をレンダリングして表示する. (rtファイルについては詳しく後ほど説明する)- rtファイルの設定が間違っている場合はエラーメッセージを表示し, プログラムを終了させる.
--saveフラグがコマンドライン引数として与えられた場合はウィンドウを表示する代わりにBMPファイル形式でレンダリング結果の画像をファイル出力する.
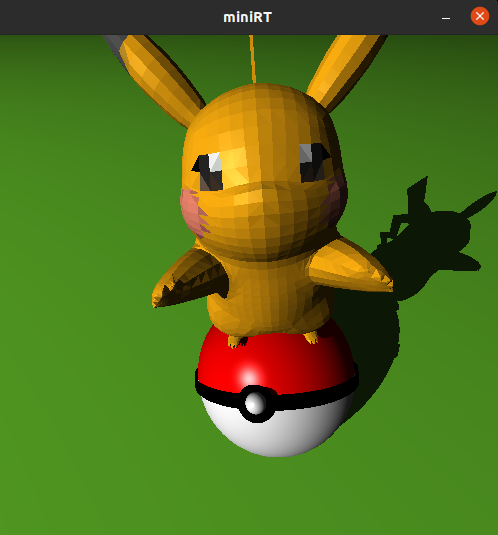
このプログラムのレンダリング結果のいくつかの例を貼っておこう.


rtファイルについて
今回のレイトレーシングプログラムはrtファイルを元にレンダリングを行うわけだが, そのrtファイルのフォーマットは以下のようになっている.
R 1024 800 A 0.1 255,255,255 c 0,3,-20 0,-0.2,1 60 c 20,3,0 -1,0,0 60 c -20,3,0 1,0,0 60 c 0,20,0 0,-1,0 60 c 0,-20,0 0,1,0 60 l 15,15,-15 0.9 255,255,255 pl 0,-4,0 0,1,0 255,255,0 sp 5,0,0 3 255,0,0 tr -3,-5,-3 3,-5,-3 0,5,0 255,255,255 cy -5,-1,0 0,1,0 4 2 0,255,0 sq 0,-2,-3 1,1,-1 3 0,176,176 sq 5,-2,-3 1,-1,1 3 100,0,176
1行が1パラメータとなっており, 形式的には先頭にパラメータの識別子(identifier)が来て, その後空白区切りでパラメータのバリューが入る.
{identifier} {param1} {param2} {param3} ...
以下に各パラメータについての説明を載せておく.
R: 解像度(Resolution)
R は解像度(Resolution)を設定するパラメータである.
R {width} {height}
width: 画面の幅height: 画面の高さ
A: 自然光(Ambient)
A は自然光(Ambient)のパラメータである.
A {lighting_ratio} {rgb}
lighting_ratio: 自然光の光の強さ. 0.0~1.0 の範囲の値.rgb: 自然光の色.
rgb についてはカンマ区切りで 255,255,255 のように指定する. 以降もrgbを受け取るパラメータがあるが, 同じである.
c: カメラ(camera)
c はカメラ(camera)のパラメータである.
c {coordinates_vec} {orientation_vec} {FOV}
coordinates_vec: カメラの座標ベクトル.orientation_vec: カメラの向きベクトル. 各x,y,z成分の大きさは -1.0~1.0 の範囲である.FOV: カメラの視野角(Field Of View). 単位はdegree.
今回 coordinates_vec や orientation_vec のように_vecのサフィックスが付いたものはベクトルを表す. 形式としては x,y,z のようにカンマ区切りで各成分を書く. この後の説明でも同じ様に _vec サフィックスのついたパラメータの設定項目が出てくるが, それらは全てベクトルを表している.
l: 光源(light)
l は光源(light)のパラメータである.
l {coordinates_vec} {brightness_ratio} {rgb}
coordinates_vec: 光源の座標ベクトル.brightness_ratio: 光源の明るさ. 範囲は 0.0~1.0 .rgb: 光源の色
pl: 平面(plane)
pl は平面(plane)のパラメータである.
pl {coordinates_vec} {orientation_vec} {rgb}
coordinates_vec: 平面の座標ベクトル.orientation_vec: 平面の法線ベクトル.rgb: 平面の色
sp: 球(sphere)
sp は球(sphere)のパラメータである.
sp {coordinates_vec} {diameter} {rgb}
coordinates_vec: 球の中心座標ベクトルdiameter: 球の直径rgb: 球の色
tr: 三角形平面(triangle)
tr は三角形平面(triangle)のパラメータである.
tr {first_coordinates_vec} {second_coordinates_vec} {third_coordinates_vec}
first_coordinates_vec: 三角形平面の1つ目の頂点の座標ベクトルsecond_coordinates_vec: 三角形平面の2つ目の頂点の座標ベクトルthird_coordinates_vec: 三角形平面の3つ目の頂点の座標ベクトル
cy: 円筒(cylinder)
cy は円筒(cylinder)のパラメータである.
cy {coordinates_vec} {orientation_vec} {diameter} {height} {rgb}
coordinates_vec: 円筒の中心の座標ベクトルorientation_vec: 円筒の向きベクトルdiameter: 円筒の直径height: 円筒の高さrgb: 円筒の色
sq: 四角形平面(sqaure)
sq は四角形平面(sqaure)のパラメータである.
sq {coordinates_vec} {orientation_vec} {side_size} {rgb}
coordinates_vec: 四角形平面の中心の座標ベクトルorientation_vec: 四角形平面の法線ベクトルside_size: 四角形平面の1辺の長さrgb: 四角形平面の色
レイトレーシングについて
実際に実装に入る前にまずはレイトレーシングとはなんぞやというのを軽く説明する.
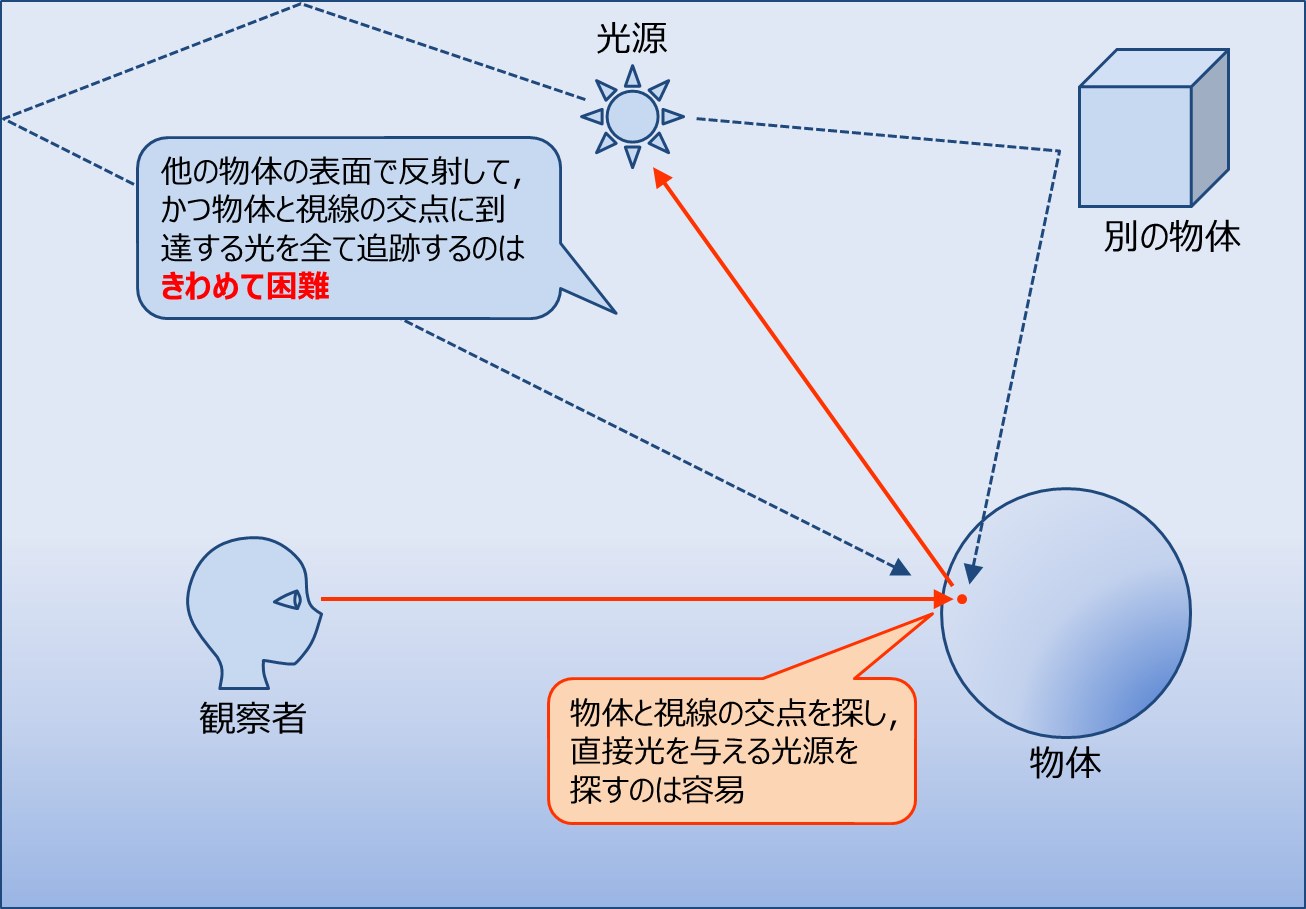
本来我々が物体を見るときには, 光源(太陽や電球)などから発した光が物体に反射し, それが目の網膜に当たり, 視神経を通じて信号として脳に伝達されて物が見える.
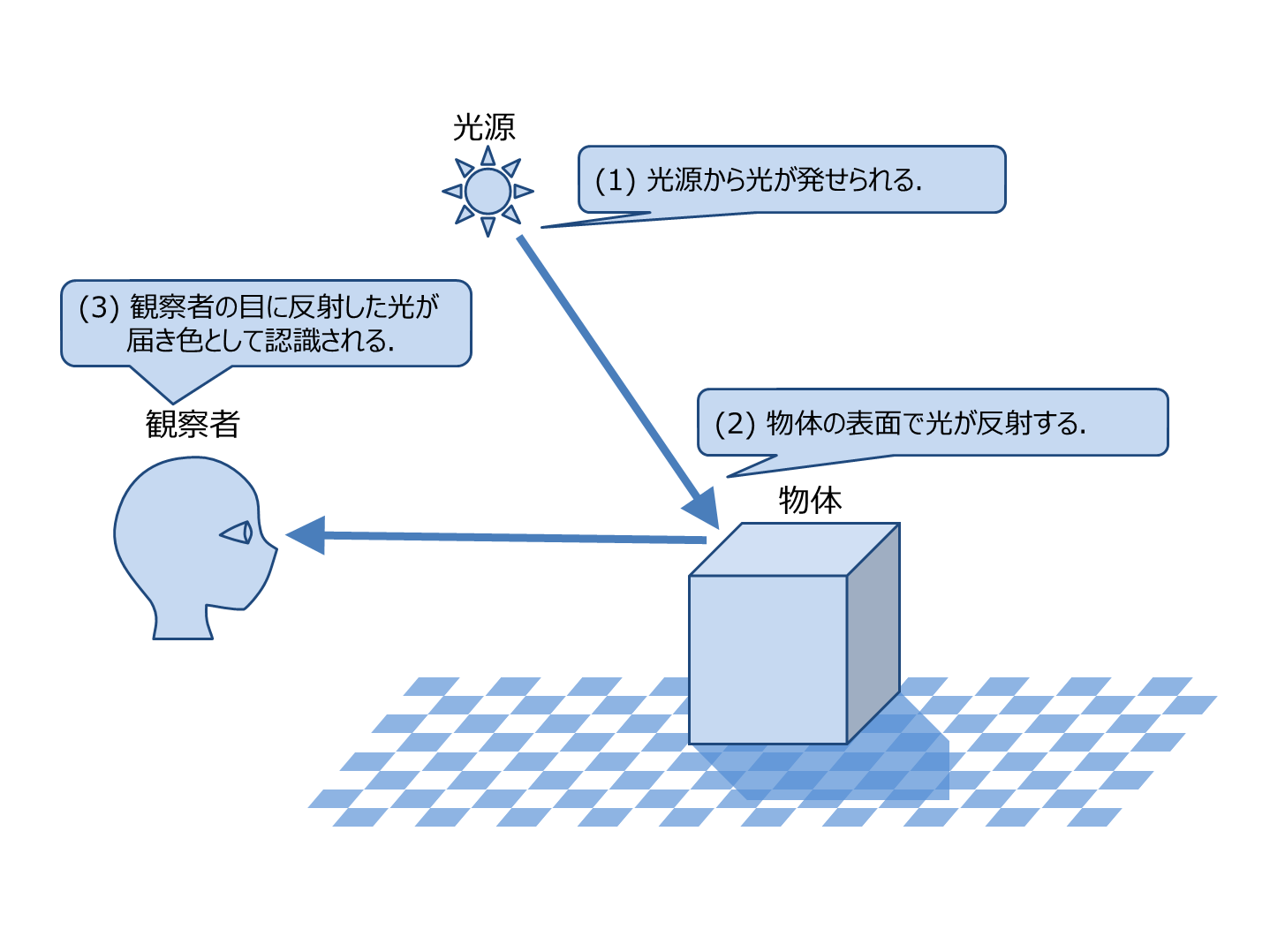 出典: The Textbook of RayTracing @TDU
出典: The Textbook of RayTracing @TDU
しかし, 光源から発せられる全ての光線を計算するのは計算量が莫大になり不可能です. また, 光源から発せられる光線の中で目に入る光線はごく一部なので, 膨大な量の無駄な計算をすることになってしまいます.
そこで, 光源から発生した光線を計算するのではなく, 逆に視点から光線を飛ばし, 「どのように目から光源まで光線が飛ぶか」をシミュレートする手法を使う. これがレイトレーシングである.
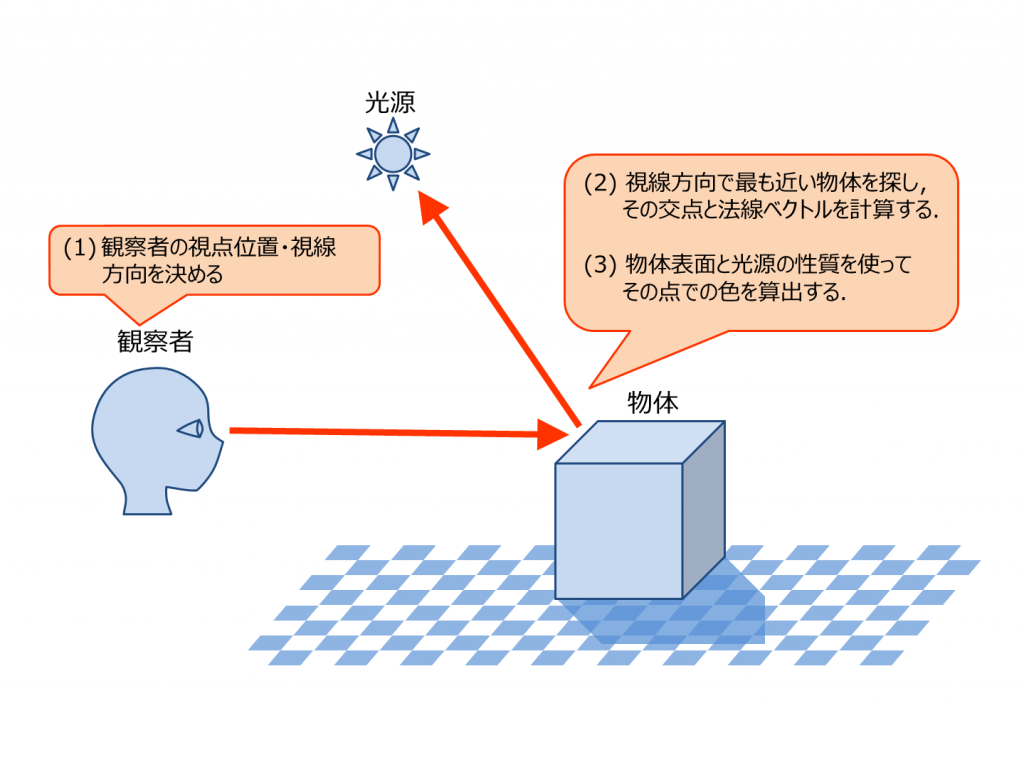 出典: The Textbook of RayTracing @TDU
出典: The Textbook of RayTracing @TDU
詳しくは画像の出典元を見てください.
また, 以下の動画もわかりやすくて良いです. (レイキャスティングの動画ですが)
ちなみに, レイトレーシングとレイキャスティングという似たような響きですが, この2つは少し違っていて, 簡単に違いを説明すると,
- レイキャスティング: 視点から放った光線がオブジェクト(壁やスプライトなど)に当たるまでの距離を計算し, その距離を元に描画する. 光の屈折や反射などは考えない.
- レイトレーシング: 視点から放った光線が光源に達するまで追跡する. その際, オブジェクト(球など)に光線が衝突した場合に発生する反射や屈折なども考慮して追跡し, その結果を元に色を計算し, 描画する. 光線がオブジェクトに衝突しなかった場合には背景色を描画する.
のようになっている.
ちなみに最近のレイトレーシングは本当に凄いので, 一度見てみると良いです.
こちらのNvidia公式のRayTracingのの説明動画も良いです.
実装
じゃあ実際に実装していくわけだが, 実装しやすい順番というのがなんとなくあるので, それを元に実装していく.
実装順としては
- プロジェクトで使う構造体とそれに関連した関数の定義
- ベクトル構造体
- 色情報構造体
- ワールド情報構造体
- レイの表し方
- 平面や球との交差判定
- 位置と向きとFOVが固定されたカメラ
- 陰影(shading)
- 環境光
- 拡散反射光
- 鏡面反射光
- 影(shadow)
- 球(
sp) - 平面(
pl) - 位置と向きとFOVが可変なカメラ(
c) - 三角形平面(
tr) - 四角形平面(
sq) - 円筒(
cy)
というような感じ. 肝となるのは 2~9 でそれ以降のものに関しては 2〜9 で実装したもと共通する部分が多い.
実際のコードは以下のリポジトリにあります.
また実装の大筋(2~8)は以下のサイトのアルゴリズムを元に実装しました.
プロジェクトで使う構造体とそれに関連した関数の定義
ベクトル構造体
C言語で実装するということで, まずベクトルの情報などを保持する構造体と, ベクトルの演算に関する関数などを作成します.
vec3.h に以下のようにベクトル構造体とベクトル演算に関する関数のプロトタイプ宣言を書きます.
// Vector3D typedef struct s_vec3 { double x; double y; double z; } t_vec3; // Vec3 Utils // 各成分を受け取ってベクトル構造体として返す t_vec3 vec3_init(double x, double y, double z); // ベクトルの足し算 a + b t_vec3 vec3_add(t_vec3 a, t_vec3 b); // ベクトルの引き算 a - b t_vec3 vec3_sub(t_vec3 a, t_vec3 b); // ベクトルの定数倍 a * b t_vec3 vec3_mult(t_vec3 a, double b); // ベクトルの内積 a · b double vec3_dot(t_vec3 a, t_vec3 b); // ベクトルの外積 a × b t_vec3 vec3_cross(t_vec3 a, t_vec3 b); // ベクトルの大きさ(長さ) |a| double vec3_mag(t_vec3 a); // ベクトルの大きさを1にしたものを返す t_vec3 vec3_normalize(t_vec3 a); // "x,y,z" の形式のテキストをパースしてvecポインタに格納して, ステータスを返す(0は成功. -1以外ならエラー) int get_vec3_from_str(t_vec3 *vec, char *str);
上記の関数の具体的な実装は以下から見れます.
色情報構造体
この先, 色の計算などを行う時にrgbを0~255ではなく0.0~1.0で計算するので, 色情報を保持する構造体と計算関係の関数をminirt.hに作ります.
typedef struct s_fcolor { double red; double green; double blue; } t_fcolor; // fcolor // t_fcolor構造体をuint32_t型に変換する uint32_t fcolor2hex(t_fcolor fcolor); // red, green, blue の値を0.0~1.0に丸める t_fcolor fcolor_normalize(t_fcolor fcolor); // 各成分から構造体の値を返す t_fcolor fcolor_init(double red, double green, double blue); // t_fcolor同士の足し算 t_fcolor fcolor_add(t_fcolor a, t_fcolor b); // t_fcolor同士の各要素同士の掛け算 t_fcolor fcolor_mult(t_fcolor a, t_fcolor b); // t_fcolor同士の定数倍 t_fcolor fcolor_mult_scalar(t_fcolor a, double b); // "r,g,b" の形式の文字列をパースして fcolor の指すアドレスに格納して, ステータスを返す(0: 成功. -1: 失敗) int get_fcolor_from_rgbstr(t_fcolor *fcolor, char *rgbstr);
ワールド構造体
プログラム実行中に物体の情報や光源情報などを保持する構造体を作ります.
typedef struct s_world { void *mlx; // minilibx特有のやつ void *win; // minilibxのウィンドウを指すポインタ int screen_width; int screen_height; t_dlist *cameras; // カメラのリスト t_list *objects; // 物体のリスト t_fcolor ambient; // 環境光の強度 t_list *lights; // 光源のリスト } t_world;
とりあえずこれで実装する準備が出来たので実際に実装していきます.
レイの表し方
ここで説明する内容は東京電機大学の資料と全く同じというか, 自分は東京電機大学の資料を見ながら実装したので, この当たりの説明は元資料である東京電機大学の資料を見た方が良いと思う. ただ, 一応ここでも軽く説明しとく.
まず, 今まで光線と言ってきたものだが, この先レイ(ray)と呼ぶことにする.
この記事の最初の方で述べたように, レイトレーシングというのは放ったレイを追跡(シミュレート)して目に入ってくる光の色や強さなどを求めるわけだが, とりあえずここでは光の強さや陰影は気にせず, 「放ったレイが物体にぶつかったかどうか」という単純な仕様を満たすことから始める.
ベクトル方程式について
様々な物体との交点を求めたい場合, 球や曲面はベクトルで表すことができ, その物体とレイとの交点を求める場合にはベクトル方程式を用いると便利である.
ベクトル方程式とは, 等式の中にベクトルが出現する方程式のことである.
もっとも簡単なベクトル方程式は以下のようなものである.
この式は と
が, 同じ向きと大きさを持つことを意味する.
なお, ベクトル方程式で注意すべきことは, 両辺ともスカラー, もしくはベクトルである式でないと意味を持たないということである.
例えば左辺がベクトル, 右辺がスカラーの以下の式は成立しない.
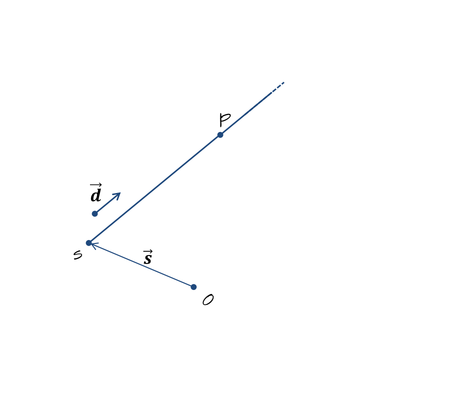
レイ(半直線) の方程式
出典: The Textbook of RayTracing @TDU
レイ(半直線)は直線と似ているが, 直線と違い終点が無い. つまり, 始点からとある方向に無限に伸びる直線である. レイは始点の位置ベクトル と 方向ベクトル
によって定義される.
レイの方程式は媒介変数を用いて以下のように表すことが出来る.
(添字付きの ,
はそれぞれ始点の位置ベクトルと方向ベクトルの成分である.)
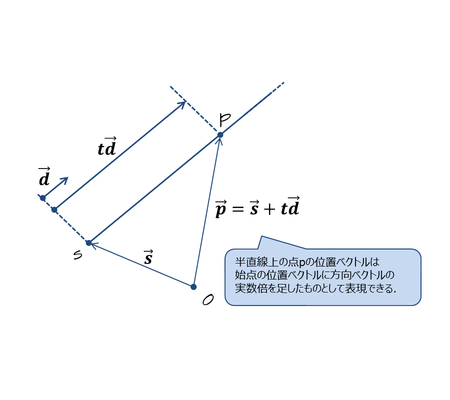
ベクトルの方程式で表すと以下のようになる.
(は点sの位置ベクトル)
文章で書けば, 半直線上の点の位置ベクトルは始点の位置ベクトルに方向ベクトルの実数倍を足したものとして表現できる ということである.
レイのベクトル方程式はこの先頻繁に出てくるので覚えておいてください.
出典: The Textbook of RayTracing @TDU
平面や球との交差判定
レイがベクトル方程式で表せるようになったので, ここから平面と球との交差判定, つまりレイと物体が衝突するかどうか, また衝突した場合の交点はどこかというのを求める.
察しのいい人は気づいているかも知れないが, 平面や球などといった物体も数式として表すことでき, それによって交点の計算が出来る.
平面
原点を通る平面の方程式とレイとの交点の求め方は東京電機大学の資料に書いてあるので省略.
ここでは任意の座標を通る平面, つまり, 任意の座標と任意の法線ベクトルを持つ平面とレイとの交差判定について説明する.
まず, 任意の座標と任意の法線ベクトルを持つ平面 というのを想像してほしいわけだが, 以下の図の って書いてあるベクトルが任意のベクトルに置き換えた様子を想像して欲しい. また, 法線ベクトルに関しては, この
が自由に向きを変えれる(平面が向いている方向を変えれる)ことを認識しておいてもらいたい.
ここから実際に任意の座標と任意の法線ベクトルを持つ平面とレイとの交差判定について説明していく.
まず, 任意の座標を通る平面の方程式というのは以下のような式である.
ここで, は法線ベクトル
のx,y,z成分を表す.
また, のように
0の添字が付いているものはの成分である.
ここで平面上の任意の点 はと平面の法線ベクトルは以下のような関係を持つことに注目する.
つまり, 平面上の任意の点と法線ベクトルの内積は必ず0になるということである.
上記の式とレイのベクトル方程式で連立方程式が立てれる.
この式をについて解くと以下の式が出てくる.
解いたをレイの方程式に突っ込めば交点の座標が出てくるわけ.
なお, の時は交点が無いと判断する.
ちなみに, の値は3つのパターンがあり,
: レイは平面との交点を持つ
: レイの始点は平面上にある
: 平面はレイの方向ベクトルの逆方向, すなわち見ている方向の反対側にある.
球
平面の交差判定の式の導出は完了したので次は球の交差判定の式を導出する.
例によって原点を通る球の方程式とレイとの交点の求め方は東京電機大学の資料に書いてあるので省略.
ここでは任意の原点を中心とした球とレイとの交点の求め方を求める.
まず, 任意の点を中心とする半径
の球は以下の式で表すことが出来る.
次に, レイのベクトル方程式と, 上記の式の右辺の式を使って連立方程式を立てて, それを解くとレイの半直線と球との交点を求める式が導ける. (正確には交点までのレイの長さを求めて, それをレイのベクトル方程式に当てはめるわけだが)
レイのベクトル方程式を球のベクトル方程式に代入する(はてなブログのTex記法で上手く数式に番号付けれん)
これを二次方程式と見做して, 以下のようにする
また判別式 [tex: D = B2 - 4AC] の値によって解の個数が変わる.
: レイと球は2つの交点を持つ
: レイと球は1つの交点を持つ
: レイと球は交点を持たない(レイと球は交差しない)
位置と向きとFOVが固定されたカメラ
ここでは単純化したカメラ. 具体的には位置と向きとFOVが固定されたカメラを定義し, またどのようにして3D空間を2D空間(スクリーン)に投影するかというのを説明しよう....と思った東京電機大学と全く同じなので詳しくは以下のサイトを見てくれ.
レイの定義
まぁ基本的には以下の2枚の画像がわかってれいればよくて
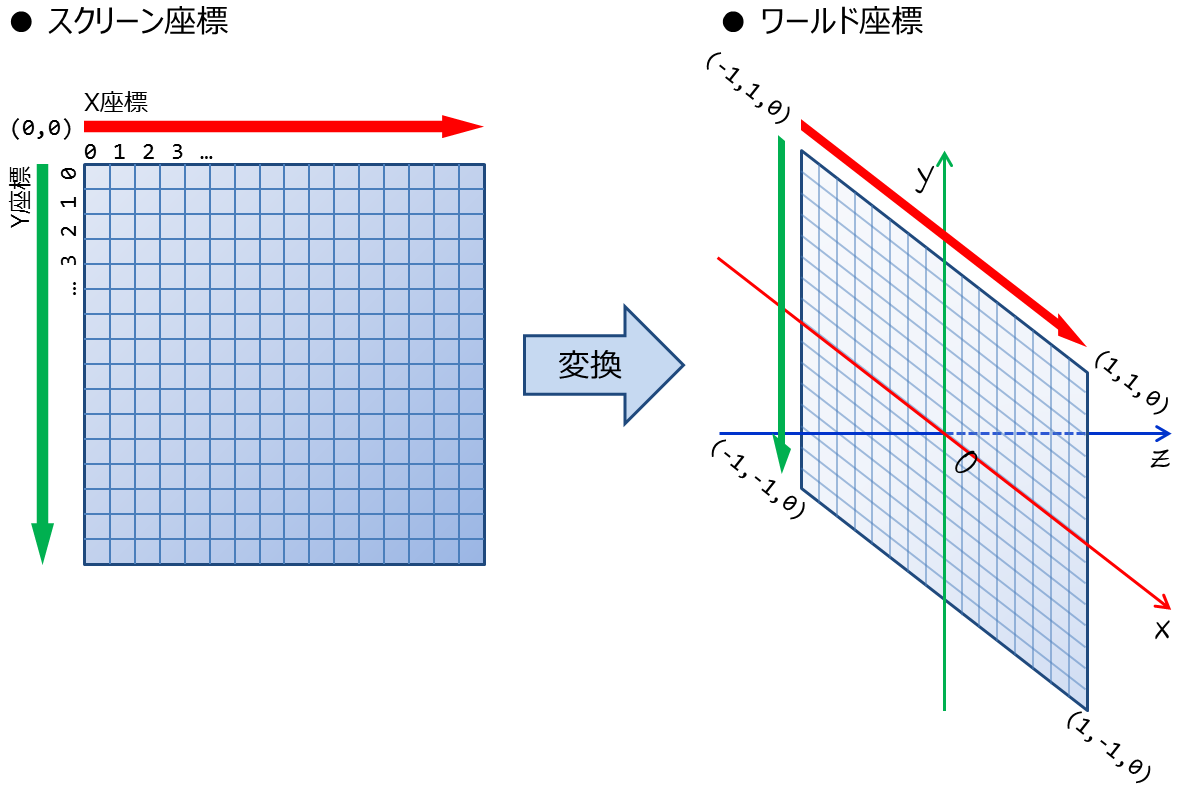
出典: The Textbook of RayTracing @TDU
この画像はスクリーン座標をワールド空間内で扱いやすいようにx,y座標を[-1.0-1.0]の範囲に正規化するのと, y座標を下向きに定義するという話.
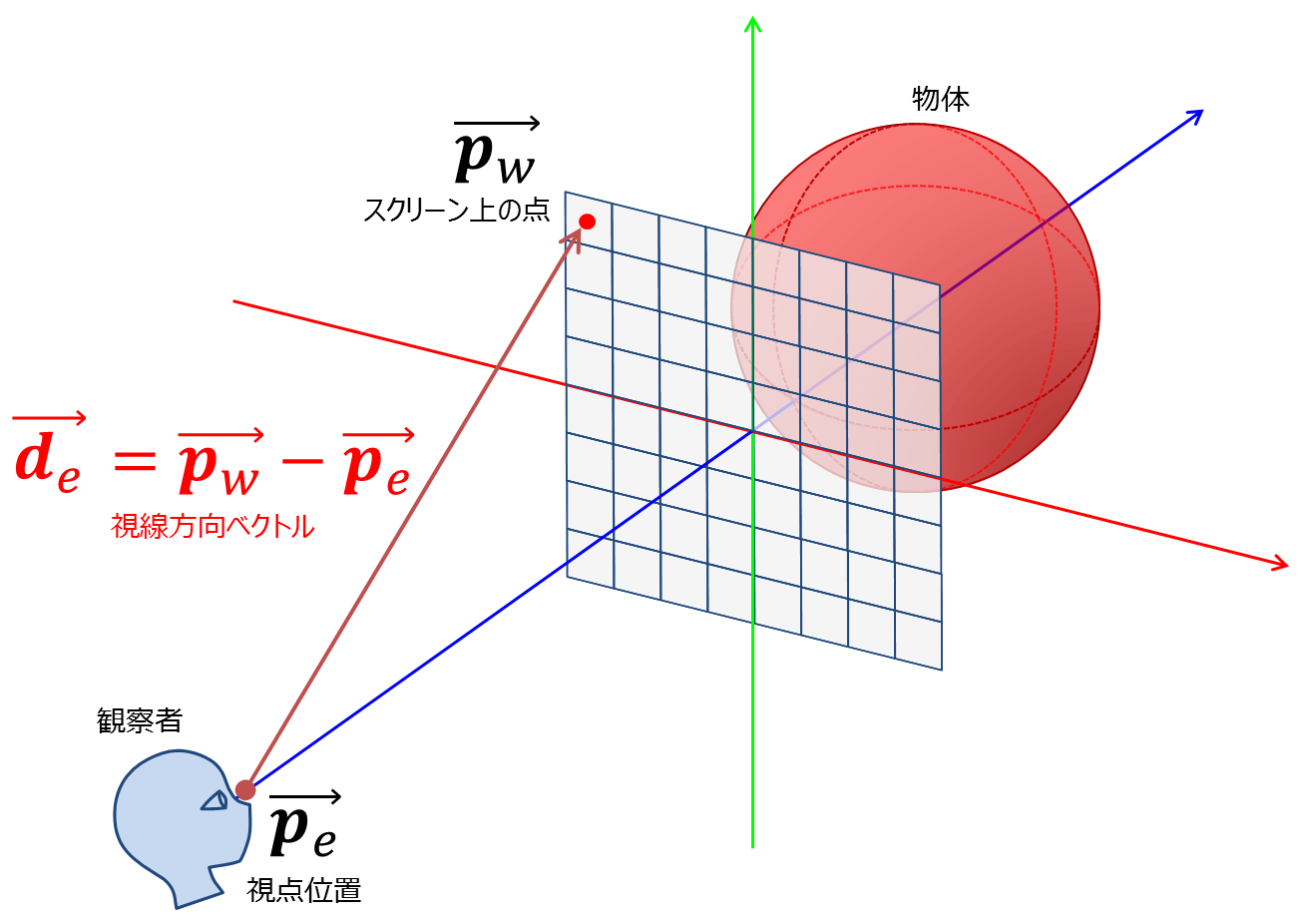 出典: The Textbook of RayTracing @TDU
出典: The Textbook of RayTracing @TDU
こっちの画像はレイの半直線をどのように定義するかという話. 今回は視点からスクリーン上の点への向きを向きベクトル として使うという話.
球とレイの交点の描画
ここではレイと球をコードとして表現し, 球との交差判定を実装する. また, 交点があったら画素を赤色にセットし, そうでなければ背景色(青色)をセットすることによって交差判定が正しく動作することを確認する.
物体とカメラの関係は以下の画像のように設定する.
出典: The Textbook of RayTracing @TDU
int raytracing(t_world *world)
{
// 視点位置を表すベクトル
t_vec3 camera_vec;
camera_vec = vec3_init(0, 0, -5); // スクリーンの少し手前な感じ
// 球の中心座標
t_vec3 sphere_vec;
sphere_vec = vec3_init(0, 0, 5); // スクリーンの少し奥な感じ
double sphere_r = 1; // 半径
for (double y = 0; y < world->screen_height; y++){
for (double x = 0; x < world->screen_width; x++){
// スクリーン座標からワールド座標への変換
// x,yは[-1,1]へ変換する
// スクリーン上の点の三次元空間における位置を計算する
t_vec3 screen_vec;
screen_vec = vec3_init(2 * x / world->screen_width - 1.0, 2 * y / world->screen_height - 1.0, 0);
// 方向ベクトル
t_vec3 dir_vec;
dir_vec = vec3_normalize(vec3_sub(screen_vec, camera_vec));
//
t_vec3 camera2sphere_vec = vec3_sub(camera_vec, sphere_vec);
// レイが球に当たったか計算する
double a = vec3_mag(dir_vec) * vec3_mag(dir_vec);
double b = 2 * vec3_dot(camera2sphere_vec, dir_vec);
double c = vec3_dot(camera2sphere_vec, camera2sphere_vec) - sphere_r * sphere_r;
// 判別式
double d = b * b - 4 * a * c;
if (d >= 0)
{
my_mlx_pixel_put(&world->img, x, y, rgb2hex(255, 0, 0));
}
else
{
my_mlx_pixel_put(&world->img, x, y, rgb2hex(0, 0, 255));
}
}
}
return (0);
}
上記コードは今まで説明してきたものをコード化したものである. なお, my_mlx_pixel_put()が謎だと思うが, これは42Tokyoで使うXWindowシステムのラッパーライブラリであるminiilbx用の関数である. この記事を読んでいる人は「x,yを指定して, そこに指定の色をセットする関数」という認識で十分である.
このコードをコンパイルして実行すると以下のような画像を出力する.

陰影(shading)
前のセクションで球の交差判定を実装し, 正しく描画出来ました. 次に実装するのは陰影(shading)です.
ちなみにこのセクションの内容は例によって東京電機大学の資料とほぼ同じなので元資料読んだほうがわかりやすいと思います.
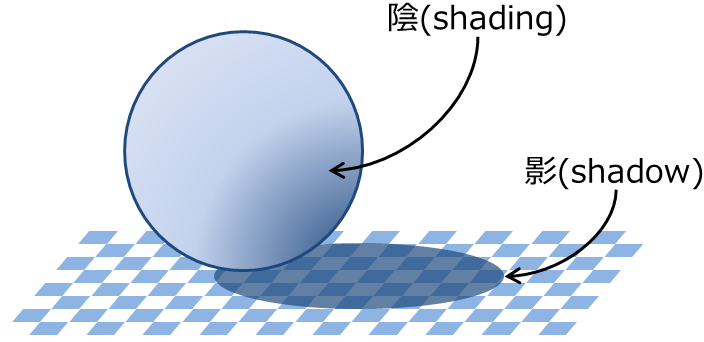
まぁそれはそれとして, 陰影とはなんぞやって感じなんですけど, それは以下の画像を見れば大体わかるかなぁと思います.
出典: The Textbook of RayTracing @TDU
光が物体表面に当たることで発生する明暗のコントラストみたいな感じかな?
これを実装するためにPhongの反射モデルと呼ばれる手法を使う.
Phongの反射モデルはWikipediaの説明と以下の東京電機大学の資料を見ると概要はなんとなくわかると思います.
出典: The Textbook of RayTracing @TDU
Phongの反射モデルでは, 2種類の光源の種類がある.
- 環境光(Ambient): シーン全体を照らすような光源で, 別の物体表面での反射を経て物体表面に届く光のこと. イメージとしては太陽みたいな感じ.
- 直接光(light): 電球のようなある場所から光を放つような光源. イメージとしては白熱電球みたいなイメージ
この光が当たることによって物体表面に陰影が出来る. 物体に当たった光が反射して目に見えるわけだが, Phongの反射モデルではその反射光を以下の3つの要素の総和で近似する.
- 環境光の環境反射(Ambient)
- 直接光の拡散反射(Diffuse)
- 直接光の鏡面反射(Specular)
 Brad Smith投稿者自身による作品 CC 表示-継承 3.0リンクによる
Brad Smith投稿者自身による作品 CC 表示-継承 3.0リンクによる
ではここからこの3つの反射現象を扱うわけだが, その前に物体の材質を定義することを忘れてはいけない. 材質と言っても鉄とか木材とかの材料の話ではなく, 光の反射係数のことである.
物体は材質として以下のパラメータを持つ.
: 鏡面反射係数. 当たった光に対して鏡面反射をどのくらいするか. RGBそれぞれのチャンネルに対して [0.0, 1.0] の値を持つ.
: 拡散反射係数. 当たった光に対して拡散反射をどのくらいするか. RGBそれぞれのチャンネルに対して [0.0, 1.0] の値を持つ.
: 環境反射係数. 自然光に対して環境反射をどのくらいするか. RGBそれぞれのチャンネルに対して [0.0, 1.0] の値を持つ.
: 材質の光沢度. 光沢のある点から反射する光がどのくらい均等に反射するかを決める. より滑らかな表面ほど大きい. また, この定数が大きければ鏡面ハイライトが小さく強くなる.
自分の実装では以下のような構造体でこれらのパラメータを保持するようにした. (環境光反射係数は1に固定しているので構造体で保持していない)
typedef struct s_material { t_fcolor kDif; // 拡散反射係数 // これを物体の色とする t_fcolor kSpe; // 鏡面反射係数 float shininess; // 光沢度 } t_material;
環境光
環境光だが, 直接光以外の光を正確に追跡することは極めて困難であるため定数として処理する.
出典: The Textbook of RayTracing @TDU
式にすると, 環境光の反射輝度は以下のように近似する.
自分の実装では はRGBの全てのチャンネルにおいて1と定義したので以下のように簡略化出来る.
拡散反射光
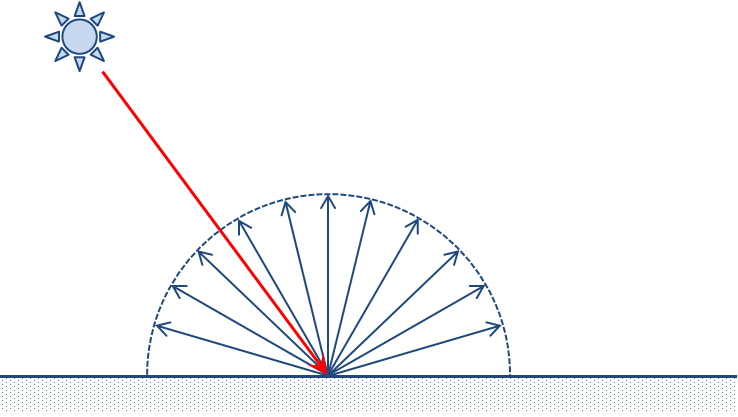
直接光の拡散反射光は, 光が物体表面で入射点からあらゆる方向に錯乱する現象である(乱反射とも言う). 拡散反射光は全包囲に広がるため, 理想的な拡散反射では反射した光の強さは観測者の視点位置に依らない.
出典: The Textbook of RayTracing @TDU
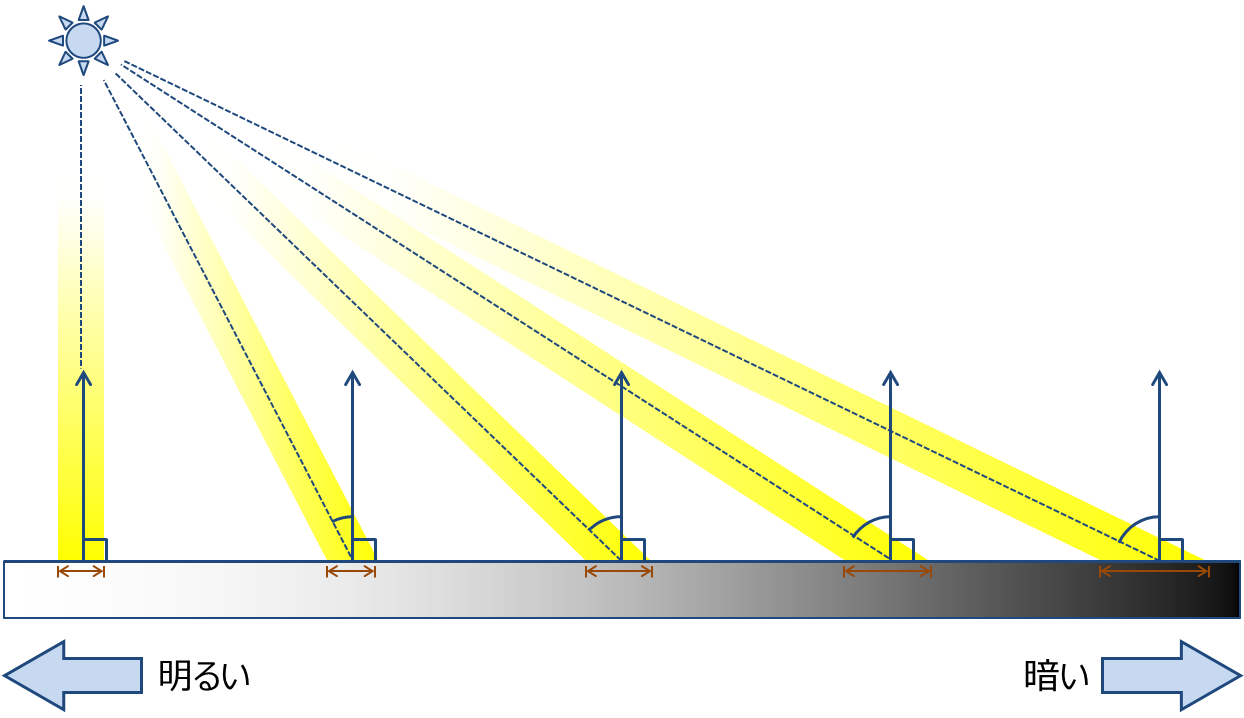
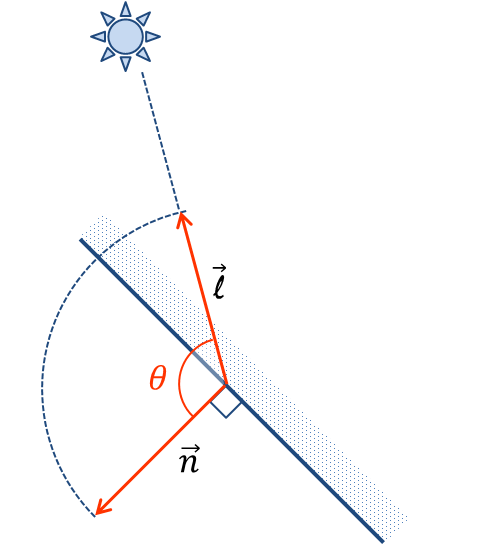
反射光の光の強さはランベルトの余弦則(Lambert's cosine law)に従うことが知られている.
ランベルトの余弦則: 理想的な拡散反射面や拡散放射体で観測される放射強度あるいは光度が, 入射光と面の法線との間の角度θの余弦(cos)と正比例することを示す法則.
出典: The Textbook of RayTracing @TDU
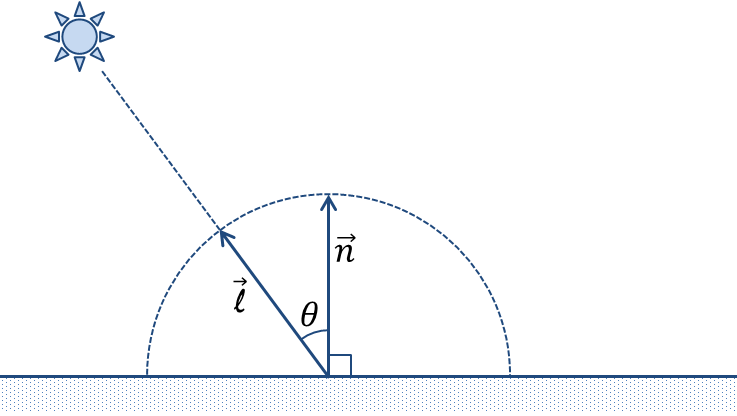
この法則に従えば を反射面の法線ベクトル,
を光の入射ベクトル,
を光源の強度,
を拡散反射係数とすると物体上のある点における拡散反射光
の強さは以下のように表現出来る.
ここで, である必要があることに注意せよ. また,
は(呼び名に反して)交点から光源に向かうベクトルであることに留意せよ.
出典: The Textbook of RayTracing @TDU
ここでなぜ角度が が角度を表すのかがわからない人は内積の定義を思い出して欲しい.
(まぁこの辺の導出は東京電機大学の資料に詳しい導出とか載ってるのでわからない人はそっち見てください)
また, 法線ベクトルと入射ベクトルのなす各が90°()を超える時, すなわち光源が面の裏から当たっているときには反射は起こらない.
実装では の時拡散反射光の反射輝度は0として扱う.
出典: The Textbook of RayTracing @TDU
鏡面反射光
次に鏡面反射について説明する.
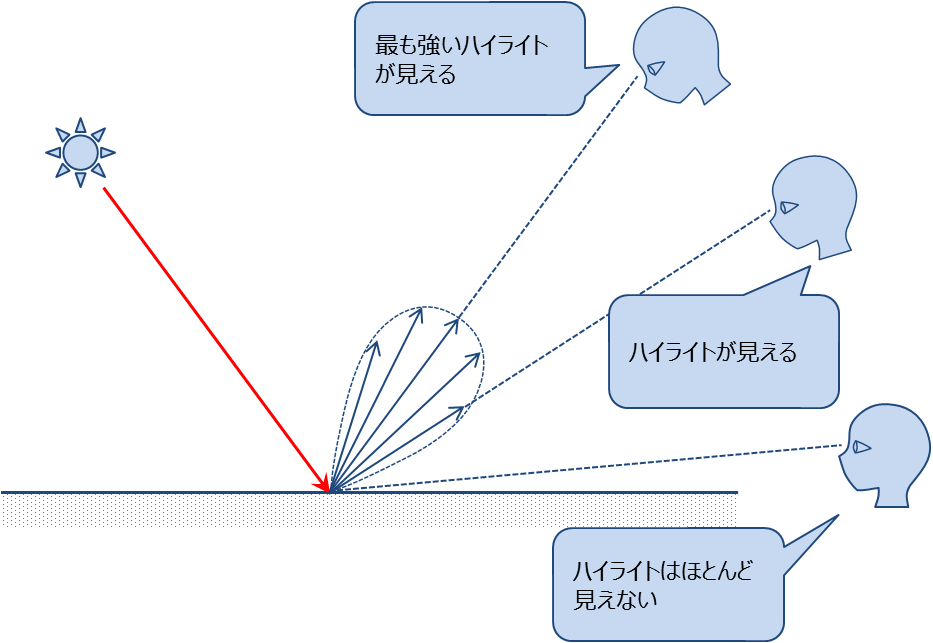
そもそも鏡面反射とは金属やプラスチックなどのなめらかな表面で起こる反射である. このような表面では光源に近い部分に明るい部分(ハイライト)が見える.
理想的な鏡面では, 光は入射角の正反射方向にのみ反射するけど, 現実は正反射方向にを中心とした範囲に反射光は広がる. また, 鏡面反射光は拡散反射光と違い全ての方向に同じ様に反射(乱反射)しないので, 鏡面反射光の強さは視点に依存して変化する.
Phongの反射モデルでは鏡面反射光の放射強度は以下のような式で近似する.
ここで,は鏡面反射係数,
は入射光の強度,
は視線ベクトルの逆ベクトル,
は入射光の正反射ベクトル,
は
と
のなす角,
は光沢度(shininess)といいハイライトの鋭さを決める係数(
)である(図10).また,
である.
この式では と
の成す角
が小さくなるほど大きくなる. つまり, 鏡面反射光が強くなる
また, が大きい値になるほど
の値の変化は急激になる. つまり,
の値が大きいほど環境反射光の範囲が小さくなる.
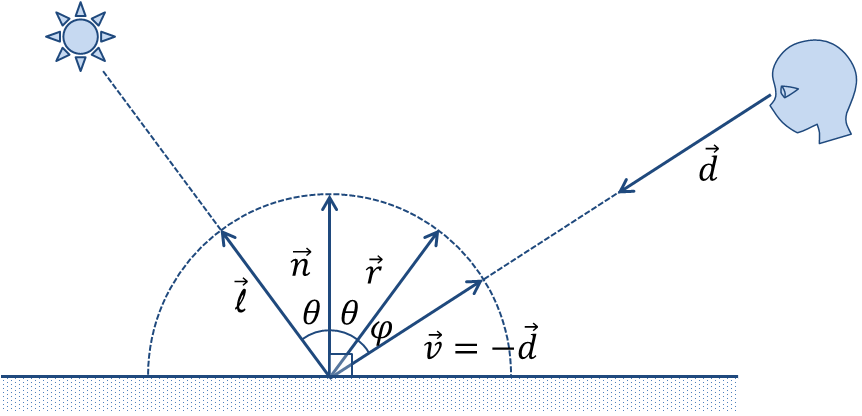 Chapter5. 陰を付ける | The Textbook of RayTracing @TDU
Chapter5. 陰を付ける | The Textbook of RayTracing @TDU
自分の実装で例を見せるとの値が変化することによって以下のように変わる.

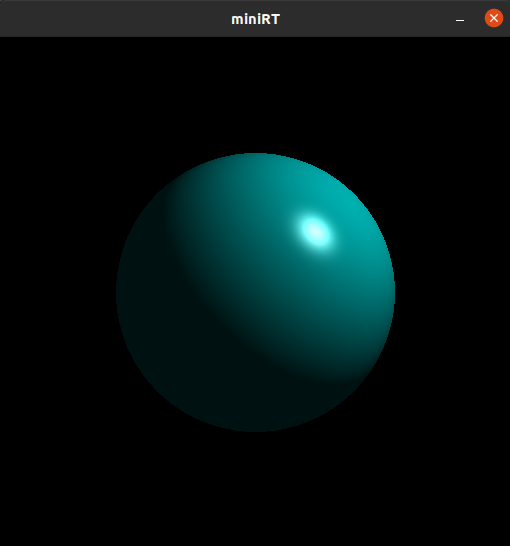
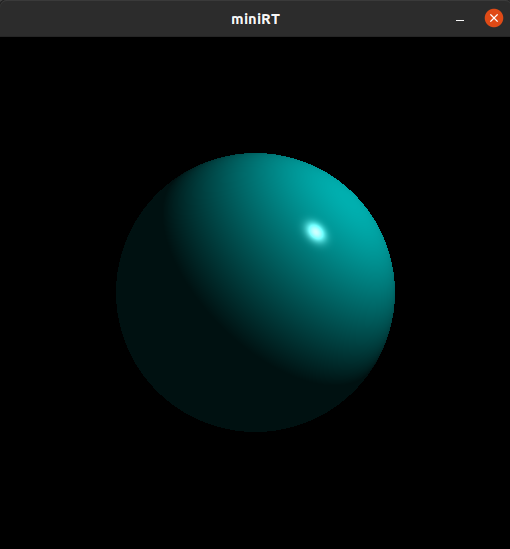
, 中央:
, 右:
拡散反射光と同じ様に, 法線ベクトルと入射ベクトルの成す角がより大きい時, つまり
の時は光が当たらないので環境反射光もゼロになる.
また, 視線ベクトルの逆ベクトル と正反射ベクトル
の成す角
が
より大きい時, つまりは
の時は環境反射光が起こらない(環境反射光がゼロという扱い).
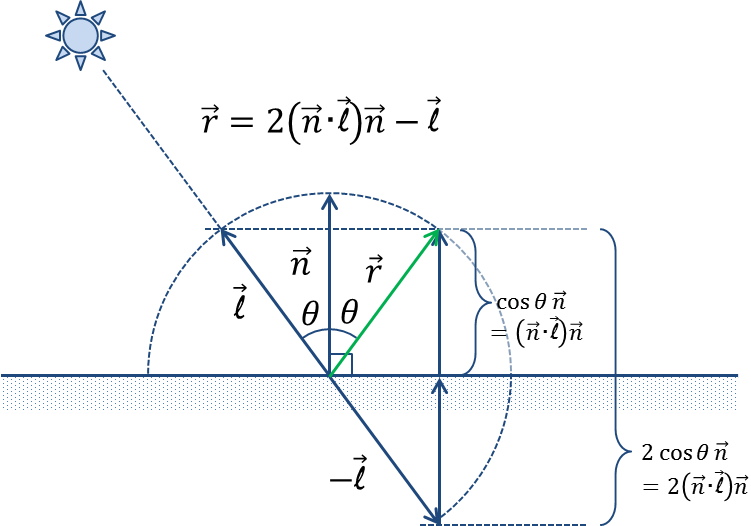
なお正反射ベクトル は以下のように計算することが出来る
Chapter5. 陰を付ける | The Textbook of RayTracing @TDU
実装について
ここまでで陰影にを構成する環境反射光, 拡散反射光, 鏡面反射光を見てきたが, 定数として扱う環境反射光を除き, 光の強さを求めるためには光源からの入射光ベクトルとレイのベクトル, そして物体上の点における法線ベクトルの3つの要素が必ず必要なことがわかったと思う.
入射光ベクトルは直接光が保持しているので問題ない. また, レイのベクトルも既に求め方を表した. 残りの物体上の点における法線ベクトルだが, これは各物体の交点ごとに求める必要がある.
つまり, 語弊を恐れずに言えば物体の交点の法線ベクトルを求めればどのような物体でも陰影が求められるということです.
球
球の陰影を求める方法を考えてみます.
レイと球との交点における法線ベクトルを求めれば今まで見せた反射光の式に当てはめるだけで光の強さが出てきます.
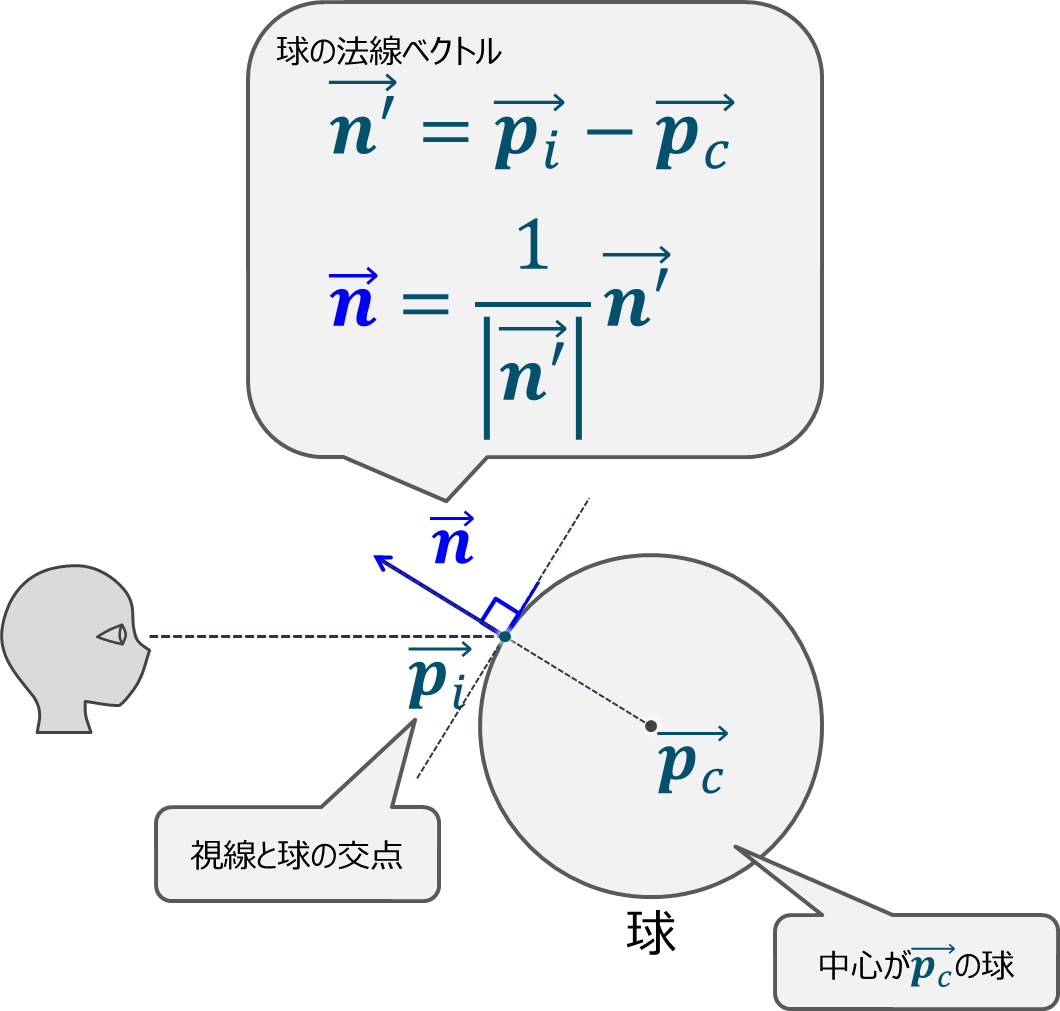
なので, ここでは球のある点における法線ベクトル を求めます.
球の法線ベクトルは球の中心ベクトルから交点へのベクトル
を大きさ1にしたものです.
 Chapter5. 陰を付ける | The Textbook of RayTracing @TDU
Chapter5. 陰を付ける | The Textbook of RayTracing @TDU
平面
平面は最初から法線ベクトルが定義されているのでそれを使えば陰影が求められます.
ここまでの実装すると以下のような画像が生成出来るようになります.

コミットにチェックアウトして実行しただけなのでちょっとバグあるけど概ねこんな感じになります. (コミットハッシュ: 9379031)
影(shadow)
陰影は計算出来るようになったので次は影の計算を計算出来るようにします.
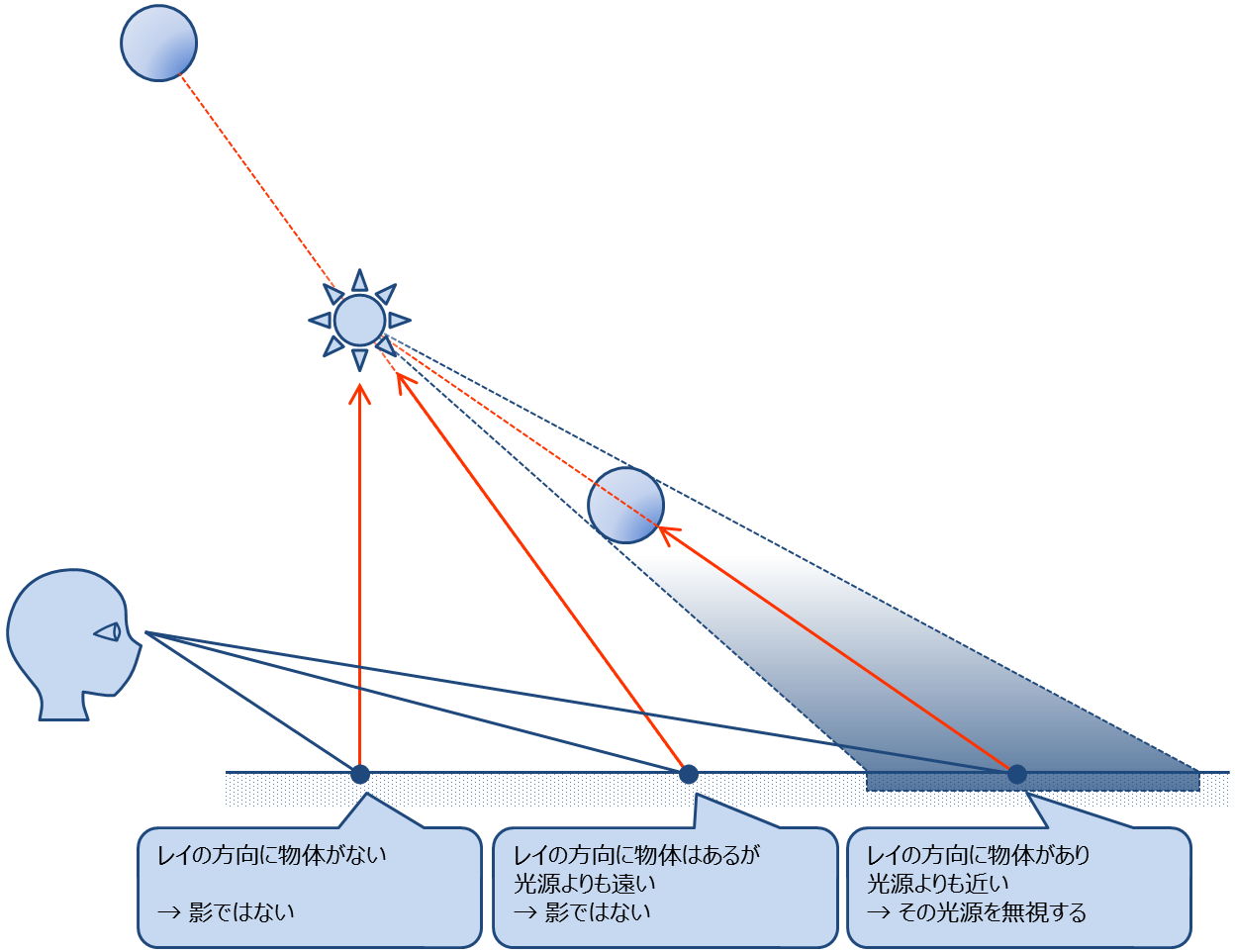
影はどのように計算するかというと, 物体とレイの交点 と 光源 の間に別の物体があれば影になります. これだけです.
交点と光源の間に物体があるかどうかは 交点を始点とし, 方向ベクトル
を
とするレイ(シャドウレイ)
をと他の物体との交差判定を行えばよい. ここで
は光源の位置ベクトルであり,
を交点の位置ベクトルとする.
交点を始点とするシャドウレイとそれぞれの物体と交差判定を行い, 交点から光源までの距離
より短いものがあれば, その交点は影になるという判定になる.
注意
シャドウレイの始点を愚直に実装すると始点が自分自身と交差してしまうので, 微小距離 をシャドウレイの始点ベクトルに足して始点をずらす必要がある.
従ってシャドウレイは以下のようになる
- 始点:
- 方向:
- 光源までの距離
ここで微小距離は適当に
や
,
などを使う.
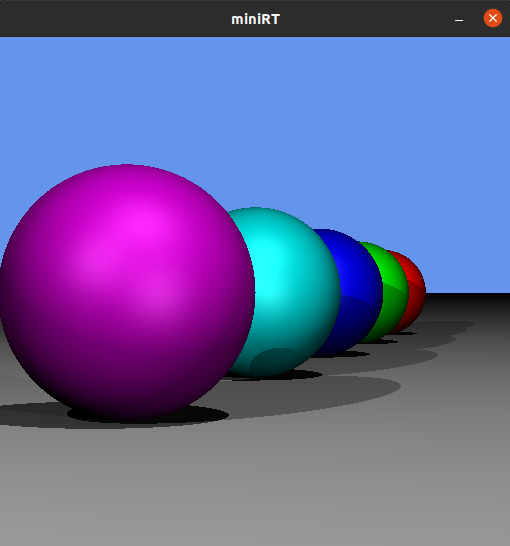
ここまで実装すれば以下のような画像が生成出来るようになる. (コミットハッシュ: 8c64c73)
球(sp)
ここまでの実装で球を描画出来る様になっている.
平面(pl)
ここまでの実装で平面を描画出来る様になっている.
位置と向きとFOVが可変なカメラ(c)
ここから先は東京電機大学の資料には載っていないので手書きの図と共に説明していく.
今までのカメラは以下の図のように位置,向き,FOV(視野角)が固定されたものだった.
Chapter4. 最初の実装 | The Textbook of RayTracing @TDU
現在の実装ではカメラの向きやFOVが変わった際に上手く動作しないので, 位置,向き,FOVが変更可能なカメラについてここでは説明する.
まず実際に詳しい説明に入る前に, 位置,向き,FOVが変更可能なカメラを機能させるために何をする必要があるのか大まかに書く
- 任意のFOVのためにカメラとスクリーンの距離
を計算する
- ワールド座標からスクリーン座標へ変換するために, スクリーン座標の正規直交基底ベクトル
,
を求める.
ではやっていくぞー.
任意のFOVのためにカメラとスクリーンの距離を計算する
任意のFOVという仕様を満たすために, 与えられたFOVによってスクリーンとカメラを近づけたり離したりして任意のFOVを実現する.
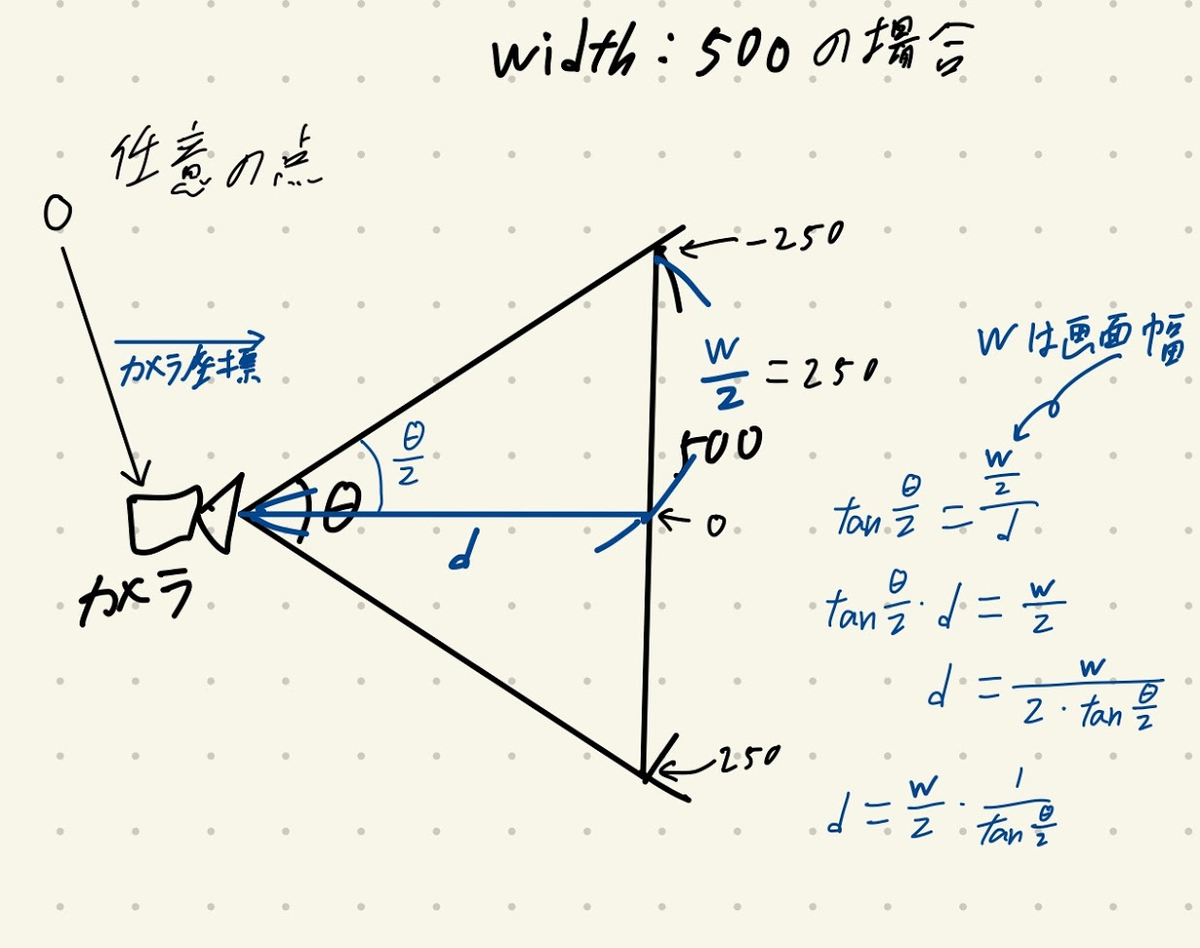
これを行うためにスクリーンとカメラの間の距離 を求める必要があるが, これは求めるのは簡単である.
与えられたFOVを とし, 画面幅を
とすると以下の式によってカメラとスクリーン間の距離を求めることが出来る.
スクリーン座標の正規直交基底ベクトルを求める
ワールド座標からスクリーン座標へ変換するために, スクリーン座標の正規直交基底ベクトル ,
を求める. と言っても訳わからないと思うので説明します.
そもそもスクリーン世界のx,yとワールドのx,yは同じではありません. 正確には基底ベクトルが異なります.
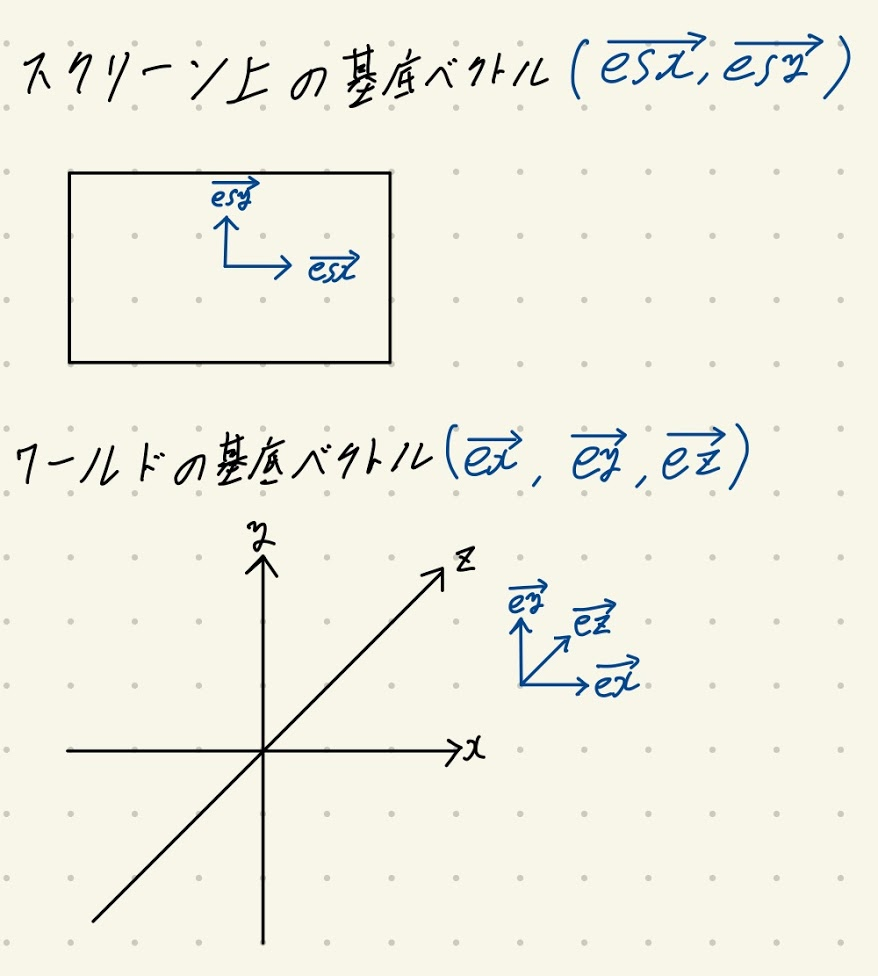
これはカメラが真っ直ぐ前を向いていない() の時, 顕著に現れます.

から
の向きに見下ろしている的な?
こういうわけなので, スクリーン座標とワールド座標を変換する処理が必要になります.
具体的には, レイはカメラの位置からスクリーンに向かってレイを飛ばす わけだが, このままではスクリーン世界の座標軸をベースなので, ワールド座標と合致せず正しく描画されません. なので, スクリーン座標軸で作ったレイの式
をワールド座標軸に変換するような処理が必要なわけです.
ではどうやって変換するかというと, スクリーン基底ベクトル,
を求めて, その基底ベクトルを使ってレイの式を立てます.
スクリーン座標からワールド座標への変換を含むレイの式は以下のようになります.
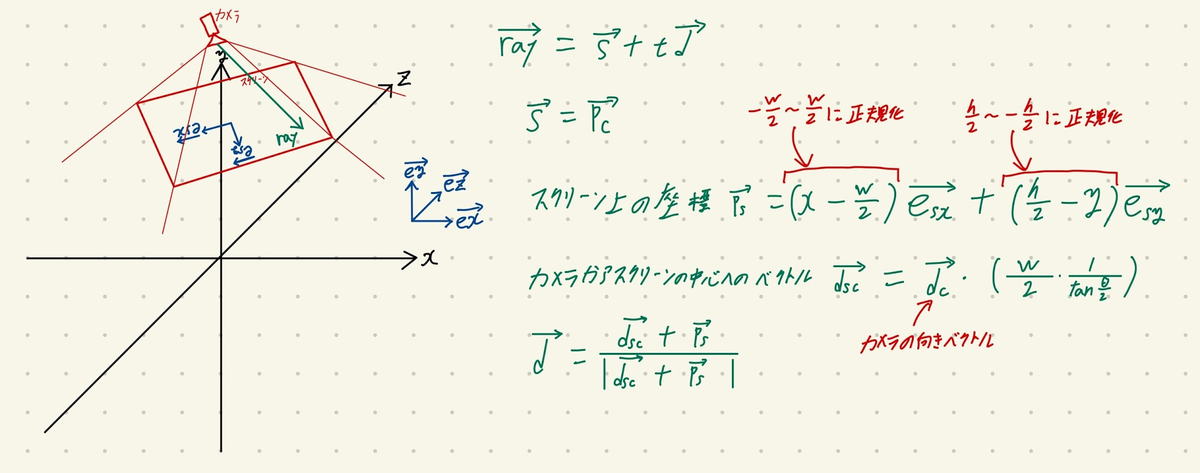
上記の最終的な式を見てわかるかもしれませんが, 基本的にスクリーン基底ベクトル ,
以外は既出の値であり, なのでここでスクリーン基底ベクトル
,
を求めてしまえばスクリーン座標からワールド座標への変換を含むレイの方程式を作成することができ, それ即ち位置と向きとFOVが可変なカメラの実装が可能になるのです.
というわけでここからスクリーン基底ベクトル ,
の求め方を説明していきます.
まず, 一つ知っておかねばならないのは, 今回の課題においてカメラに与えられるパラメータは 座標, 向き, FOV だけということです.
十分じゃね? って思うかも知れませんが, 注意せねばならないのは, 回転 が無いということです.
回転が与えられていないということはカメラは以下のように長方形に一意に決まらず, 円状になってしまうということです.
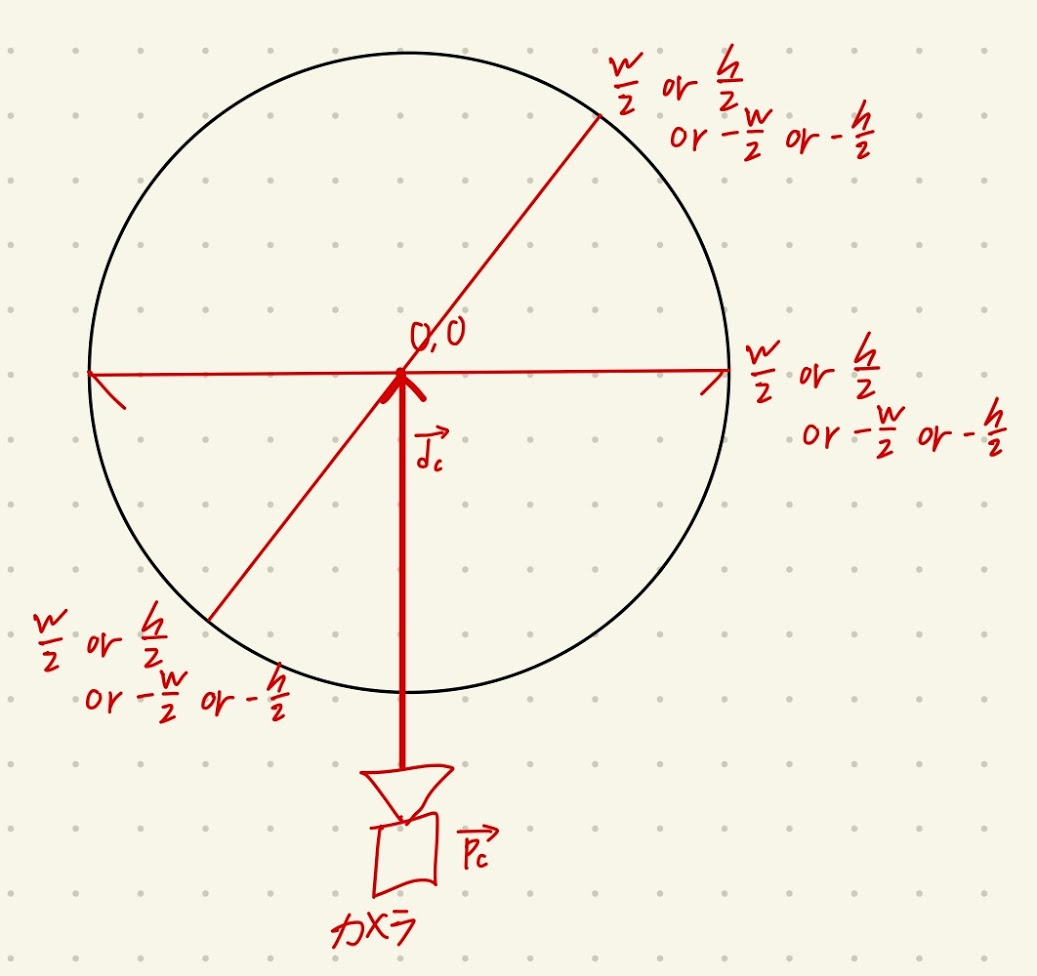
じゃあどうするかというと, こちら側で都合の良いように勝手に決めてしまいます.
どういう風に決めれば都合が良いのかというのは人によって色々あるかもしれませんが, 今回自分はワールドのx軸に水平(もしくはy軸に垂直)として勝手に決めました.
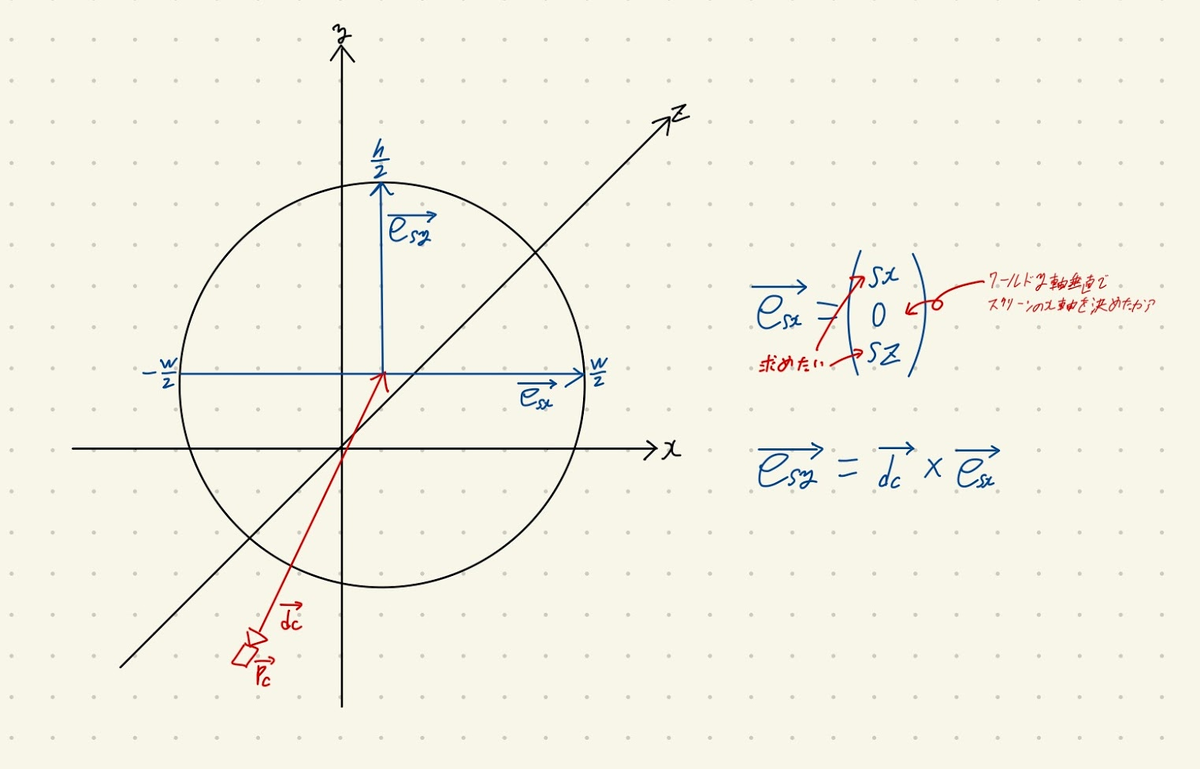
ここから を求めていきます.
はカメラの方向ベクトル
と
との外積で求めることができます.
これで のz成分である
が求められました. また, ここで
となっているところは, カメラは
側にあるので,
を使えば良いです.
③のマイナスの式を①の式に代入
これで のx成分である
が求められました. また, ここで
となっているところは, ワールド座標のx軸に合わせて
側の式を使えば良いです.
ようやく の全ての成分が求まりました!
の方はカメラの方向ベクトルと外積を取れば出てきます.
これでスクリーン基底ベクトル ,
が出てきました.
ここまで実装したら以下の画像のようにカメラの位置を自由に変えれるようになります.
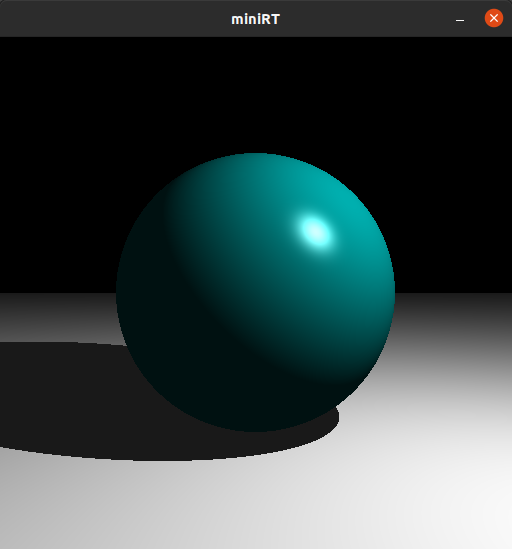
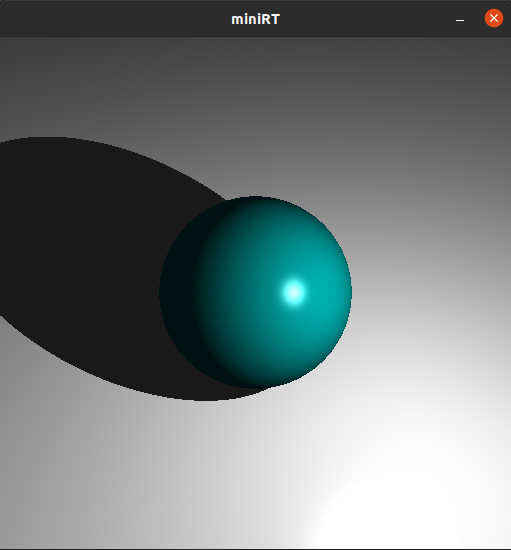
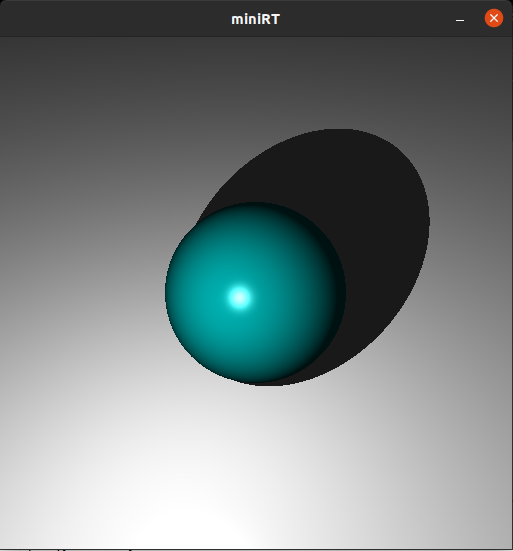
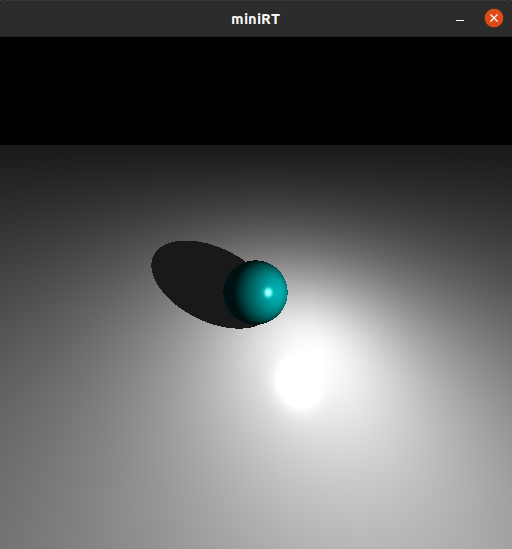
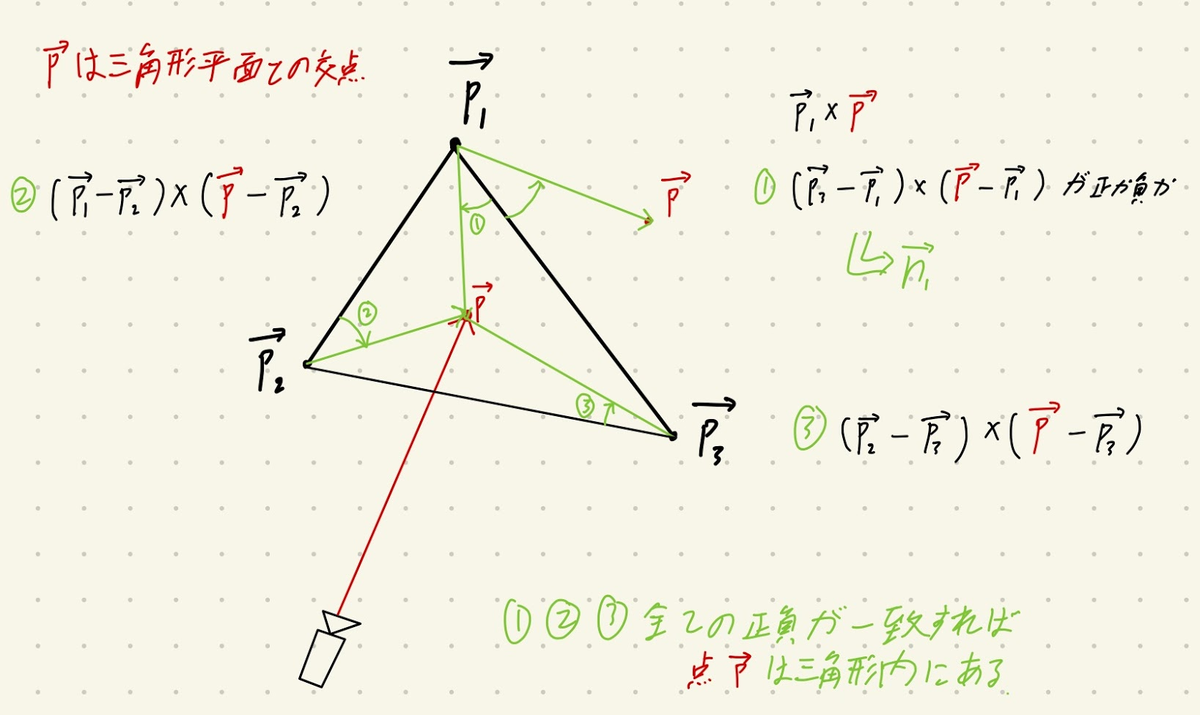
三角形平面(tr)
三角形平面は簡単です.
- 適当に三角形平面の法線ベクトルを外積を使って求める.
- 三角形の内外判定というものを行う
四角形平面(sq)
- 四角形平面を2次元で扱えるようにカメラの時と同様にワールド座標から四角形平面座標にするために四角形平面の基底ベクトルを求める
- 平面と同じ方法で交点を求める
- 求めた交点が四角形内に入っているか判定する

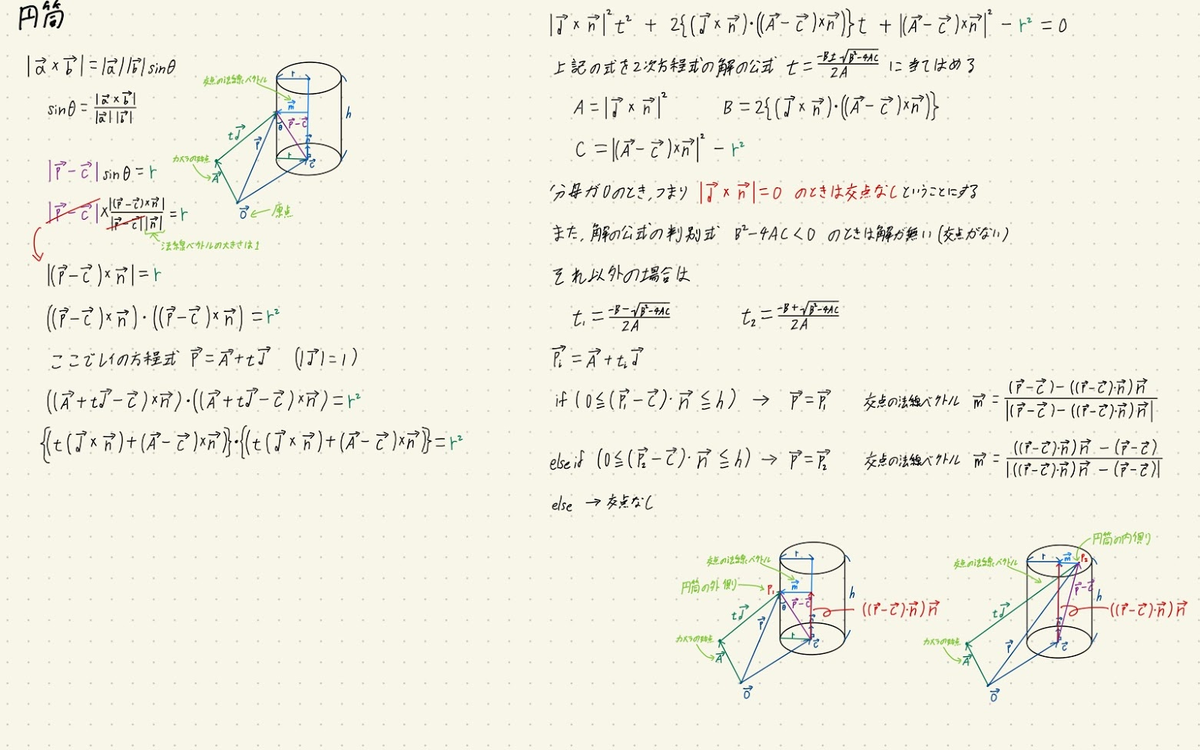
円筒(cy)
以下の画像に全て書いてます.
完走した感想
さて, 完走した感想(激ウマギャグ)ですが... 疲れたーーーーーーーーーーーーーーーーー.
miniRTの課題難しかったのでブログにまとめたいなぁと思ってまとめ始めましたが, くっっっっそ時間かかりました. ここまで書くのに14時間くらいかかりました. 疲れた.
まぁそれはともかく, 課題を完走した感想ですが, 最近流行りのレイトレーシングを自分でフルスクラッチで書くという経験はとても楽しかったです. miniRTという課題名の通り最近のNvidiaとかが出しているレイトレーシングの動画とかを見ると確かにminiなRayTraicingだなぁと思いました.
ここまで読めば解ると思いますが, とにかく数学だらけ(特にベクトル)で大変でした. 久しぶり過ぎてベクトルの外積とか調べ直してなんとか思い出して実装できました. また, 数式をコード化する作業中にバグを踏むと数式が間違っているかコードが間違っているかわからなくなりデバッグがめっちゃ大変でした.
また, 今回多くの実装は東京電機大学の資料を参考にさせて貰いました. また, カメラや円筒の実装は42の学生に教えてもらいながら実装しました. 東京電機大学, 及び42Tokyoの教えてくれた学生の皆さんありがとうございました.
というわけで, miniRTの解説記事でした.
では今日はこのへんで. ではでは〜〜👋👋